Arbitrage: Efficient Reasoning via Advantage-Aware Speculation

Monishwaran Maheswaran¹*, Rishabh Tiwari¹*, Yuezhou Hu¹*, Kerem Dilmen¹, Coleman Hooper¹, Haocheng Xi¹, Nicholas Lee¹, Mehrdad Farajtabar², Michael W. Mahoney^1,3,4, Kurt Keutzer¹, Amir Gholami^1,3

¹UC Berkeley ²Apple ³ICSI ⁴LBNL

* Equal contribution

Paper Code

TL;DR: We propose Arbitrage, a step-level speculative decoding framework that routes between draft and target LLMs based on expected quality advantage. This achieves ~2× latency reduction on math reasoning benchmarks at matched accuracy.

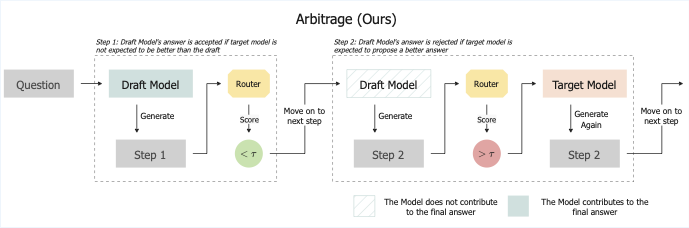
Arbitrage framework overview showing the routing between draft and target models — **Figure 1.** Arbitrage dynamically routes between a fast draft model and a capable target model based on expected quality advantage.

The Problem

Modern LLMs achieve impressive reasoning capabilities through long Chain-of-Thought generation, but this comes at substantial computational cost. Speculative Decoding (SD) offers a solution by using a fast draft model to propose tokens, which are then verified by a larger target model.

However, traditional token-level SD struggles in reasoning tasks. Minor token mismatches in semantically equivalent reasoning steps lead to unnecessary rejections. Recent step-level methods improve on this by accepting or rejecting entire reasoning steps, but they still regenerate many rejected steps with little improvement — wasting valuable compute.

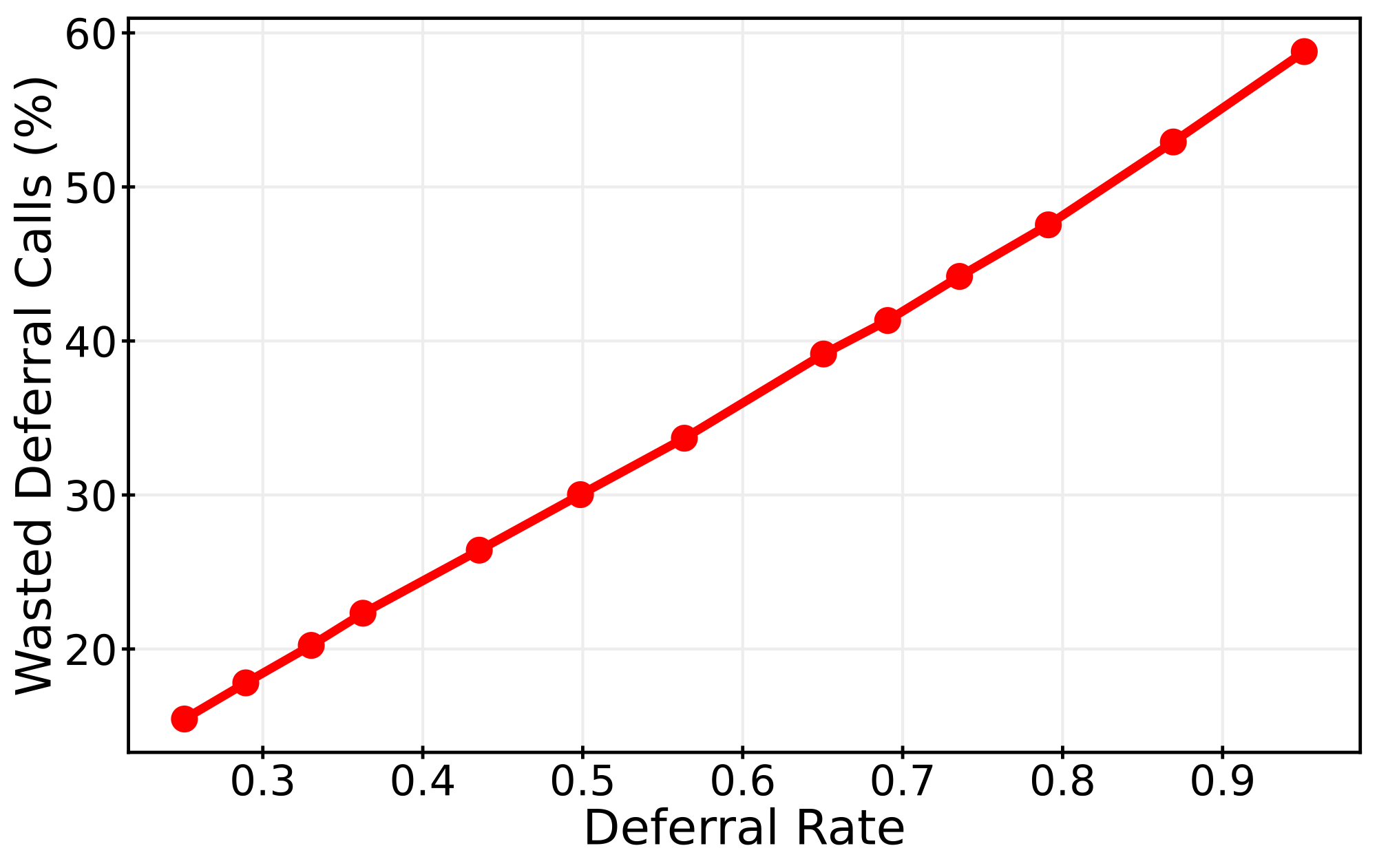
Analysis of wasted compute in existing step-level speculative decoding methods — Wasted compute: existing methods regenerate many steps that don't improve quality.

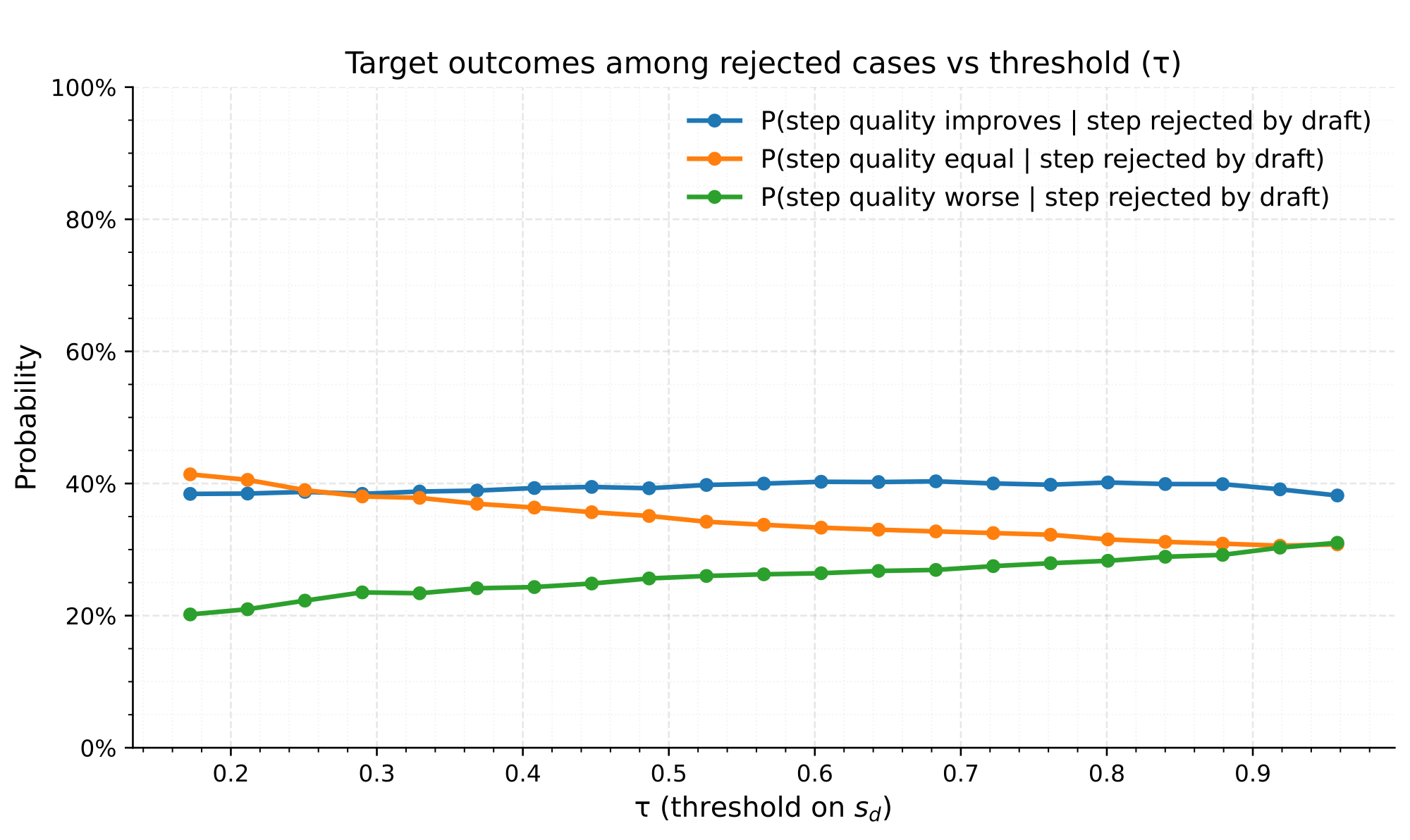
RSD outcomes analysis across different thresholds — Threshold limitations: outcome distribution varies significantly, no single threshold is optimal.

Key Insight

Existing step-level methods like RSD use a fixed quality threshold: if a draft step's quality is below some threshold, regenerate it with the target model. This is advantage-blind — it doesn't consider whether the target model would actually produce a better step.

Our key insight is simple: only invoke the target model when it's expected to provide a meaningfully better step than the draft. We call this advantage-aware routing.

Method

Arbitrage introduces two key components:

Arbitrage Oracle: A conceptual oracle that, at each reasoning step, compares draft and target continuations and greedily selects the higher-quality one. This defines a locally optimal routing policy.
Arbitrage Router: A lightweight model trained to predict the oracle's decisions. Given partial context, it estimates whether the target model is likely to produce a meaningfully better step — enabling advantage-aware routing without running the target on every step.

Case study comparing Arbitrage routing decisions with baseline methods — **Figure 4.** Case study: Arbitrage makes smarter routing decisions by considering the expected quality advantage, avoiding unnecessary target model invocations.

Results

We evaluate Arbitrage across multiple mathematical reasoning benchmarks using various LLaMA and Qwen model families. Key findings:

Up to ~2× latency reduction at matched accuracy compared to prior step-level SD baselines
Near-optimal efficiency–accuracy trade-offs that approach the theoretical oracle performance
Consistent improvements across different model scales and benchmark difficulties

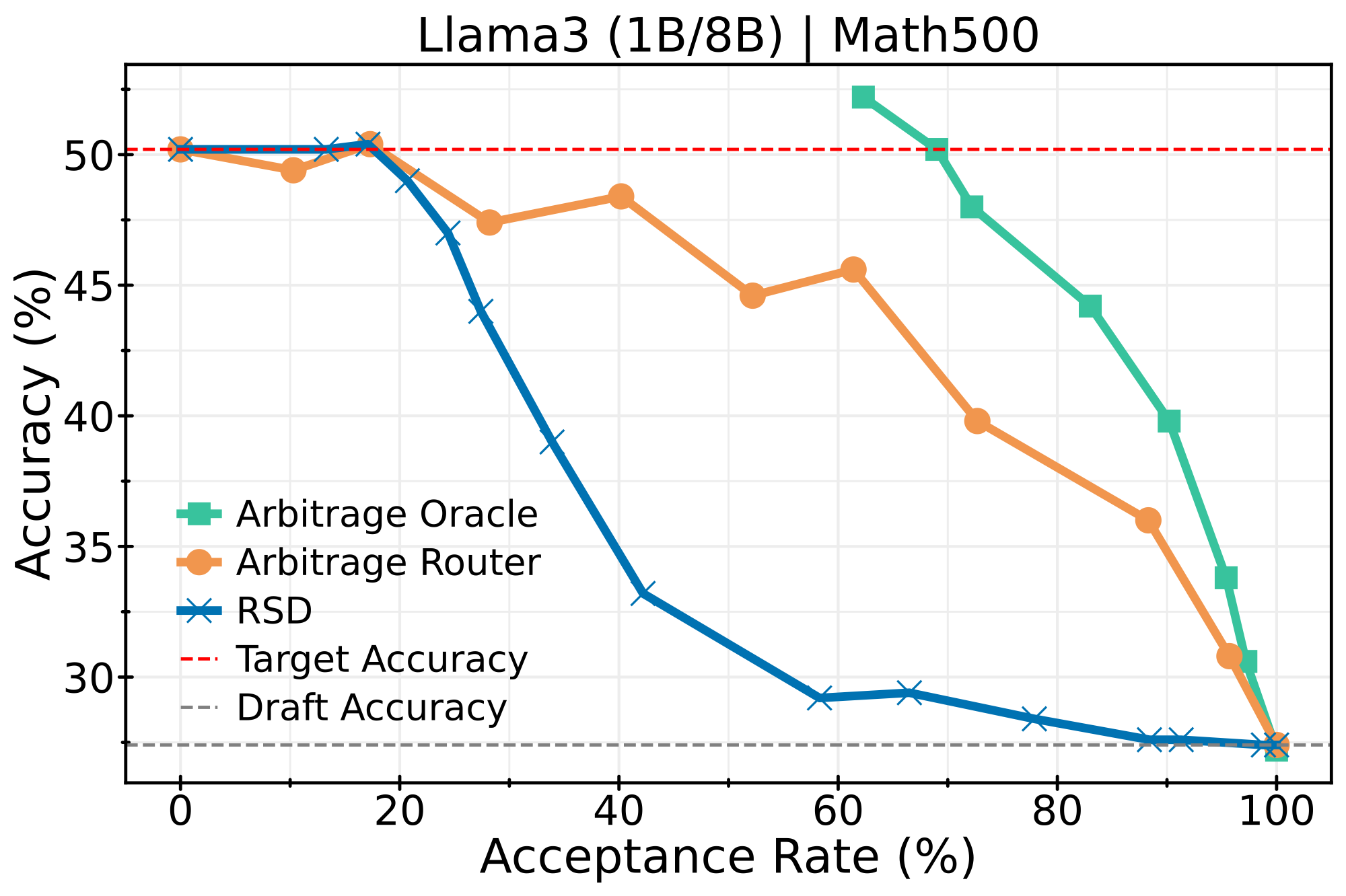
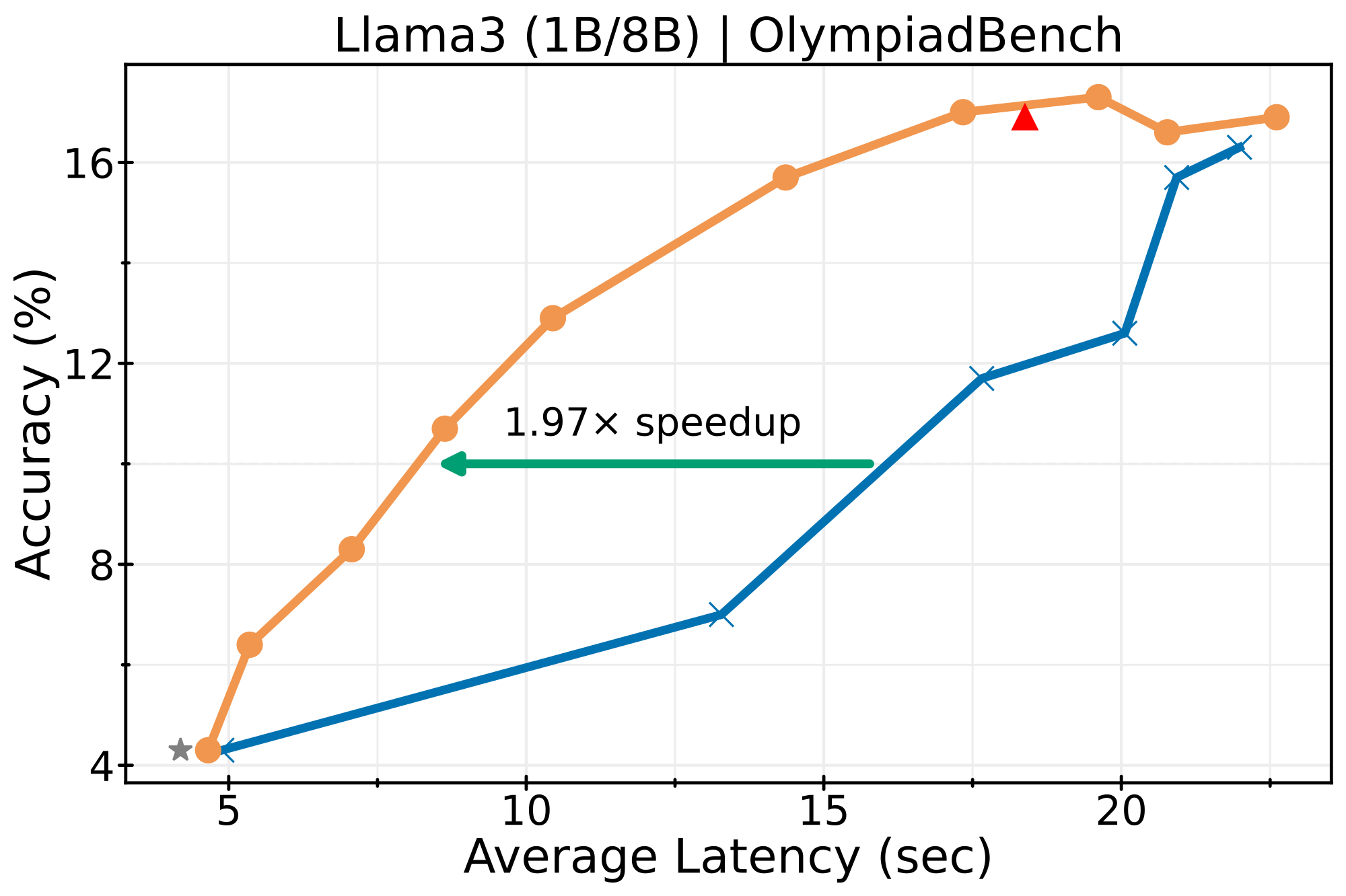
LLaMA3 (1B → 8B)

Small draft model (1B) routing to larger target (8B):

LLaMA 1B-8B on MATH500 — MATH500: Accuracy vs. Acceptance Rate

LLaMA 1B-8B on OlympiadBench — OlympiadBench: Accuracy vs. Acceptance Rate

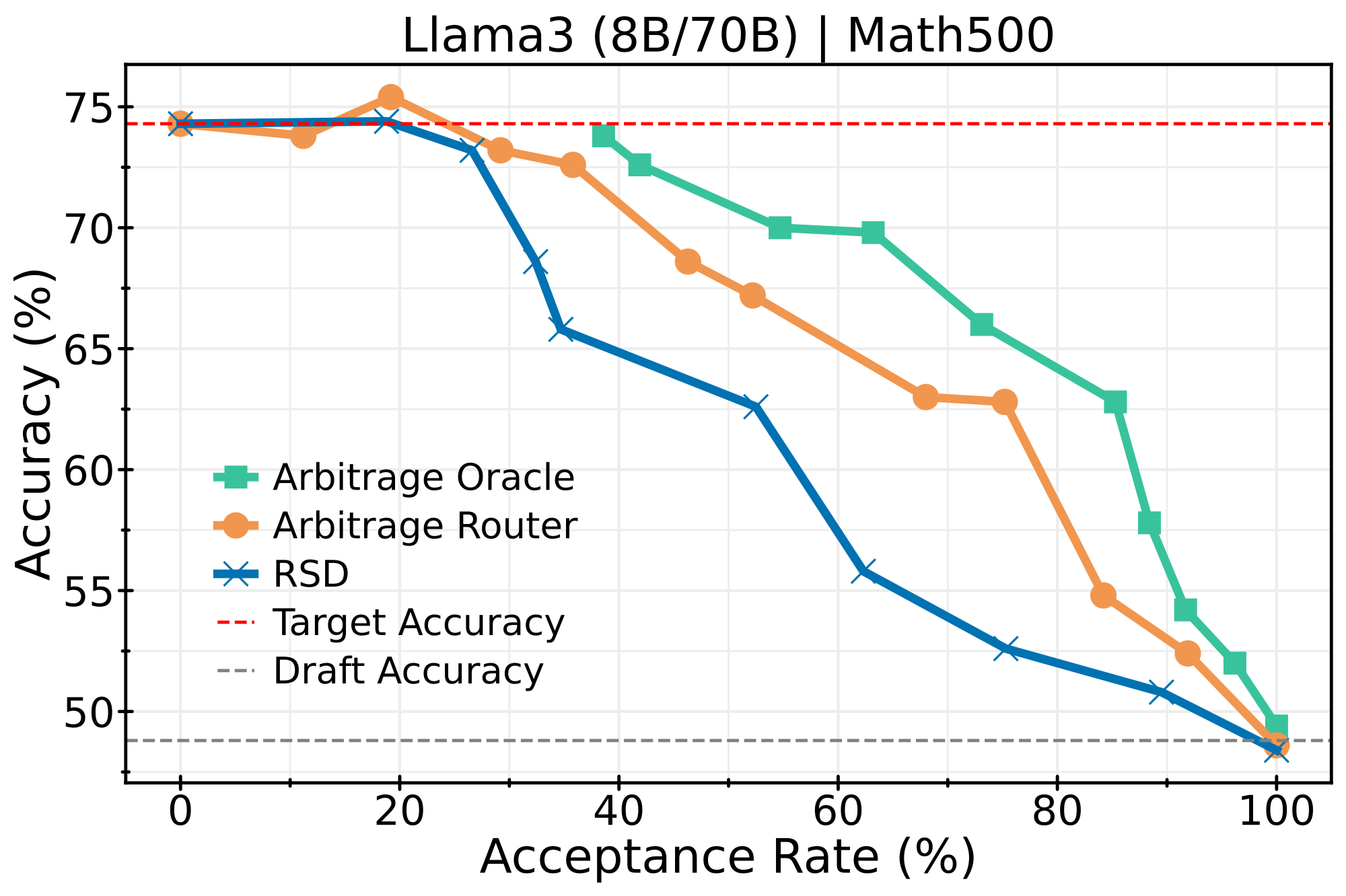
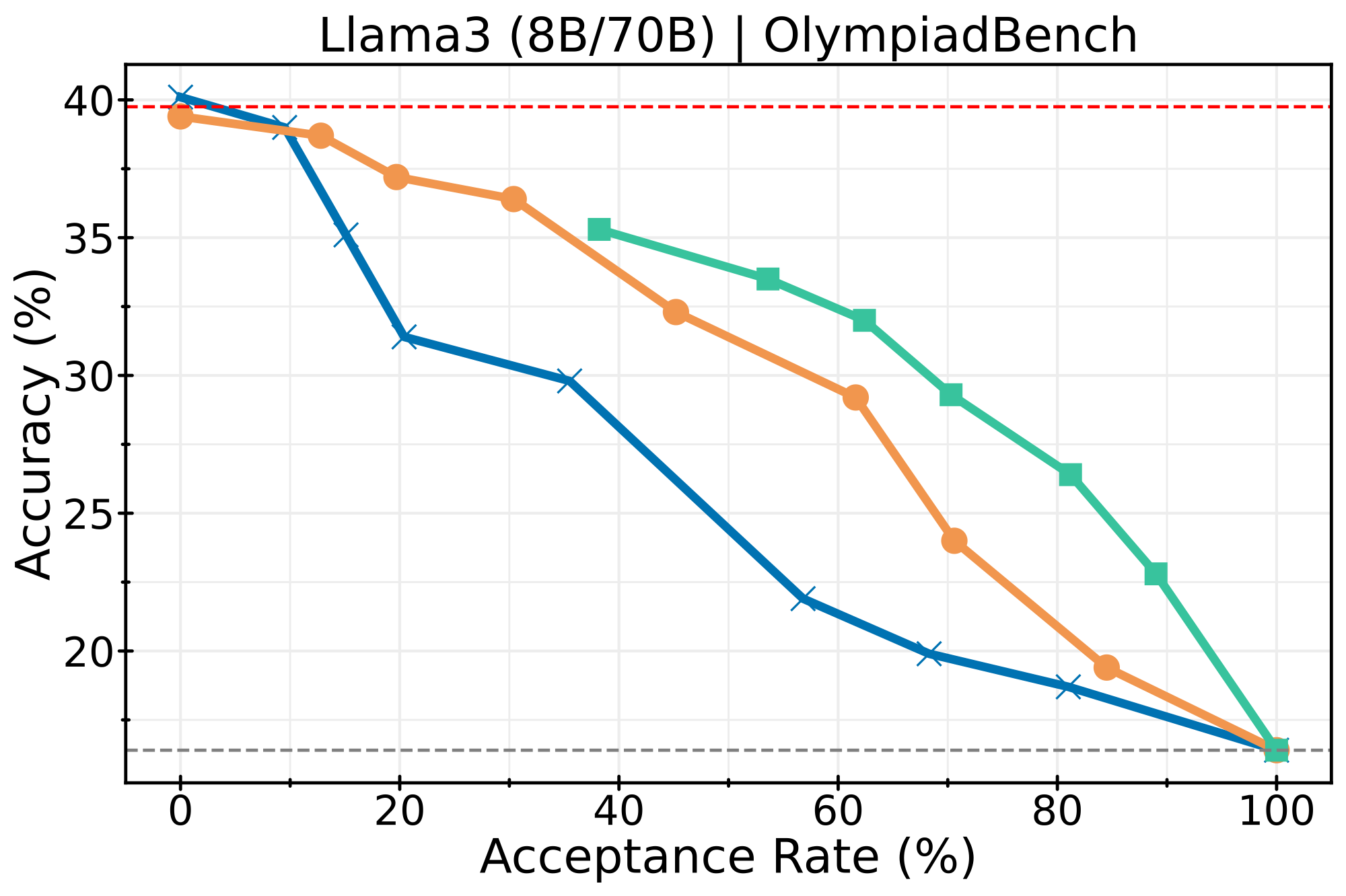
LLaMA3 (8B → 70B)

Scaling to larger models with 8B draft and 70B target:

LLaMA 8B-70B on MATH500 — MATH500: Accuracy vs. Acceptance Rate

LLaMA 8B-70B on OlympiadBench — OlympiadBench: Accuracy vs. Acceptance Rate

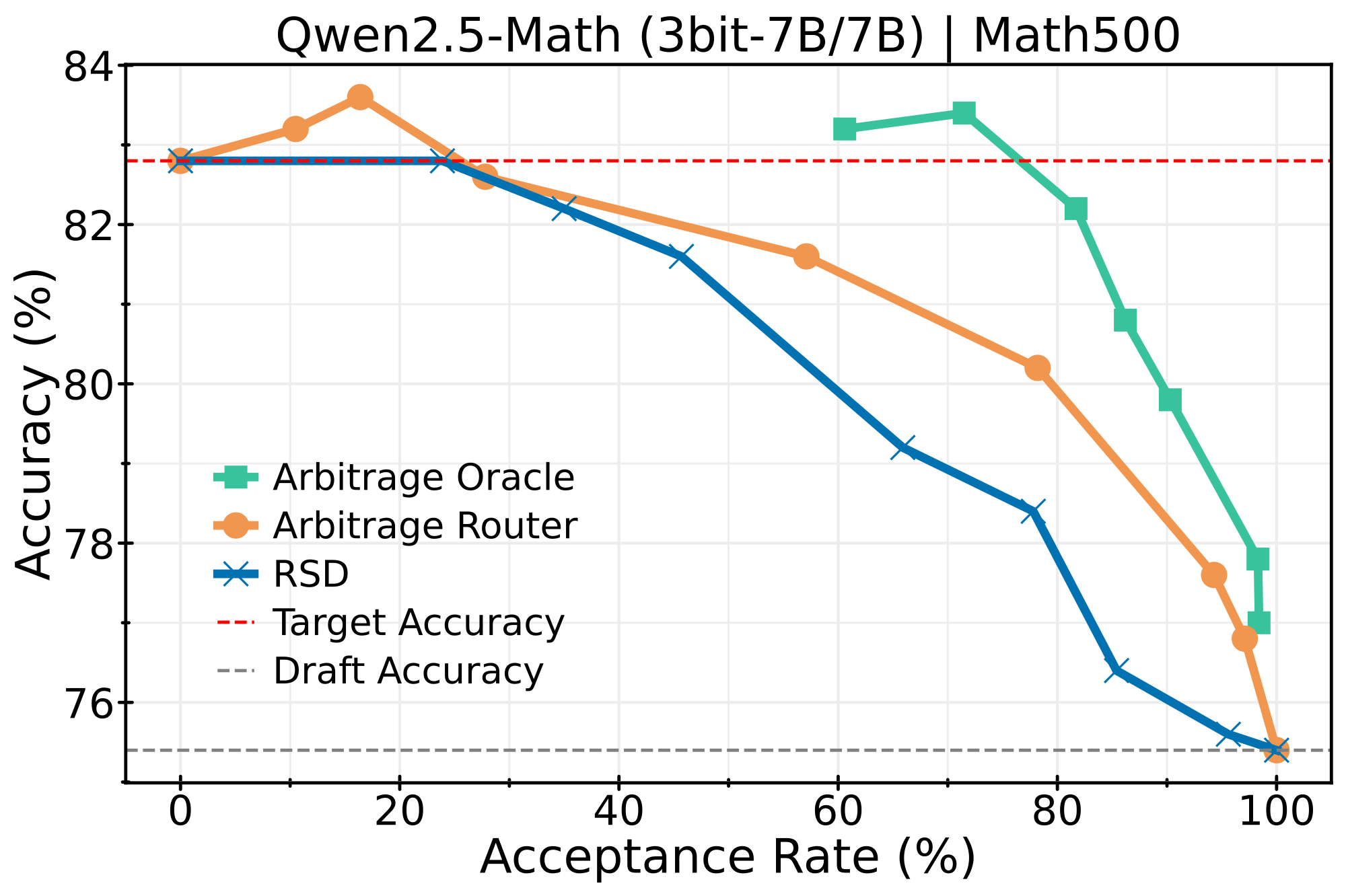
Qwen2.5-Math (3bit-7B → 7B)

Quantized draft model routing to full-precision target:

Qwen 3bit-7B to 7B on MATH500 — MATH500: Accuracy vs. Acceptance Rate

Qwen 3bit-7B to 7B on OlympiadBench — OlympiadBench: Accuracy vs. Acceptance Rate

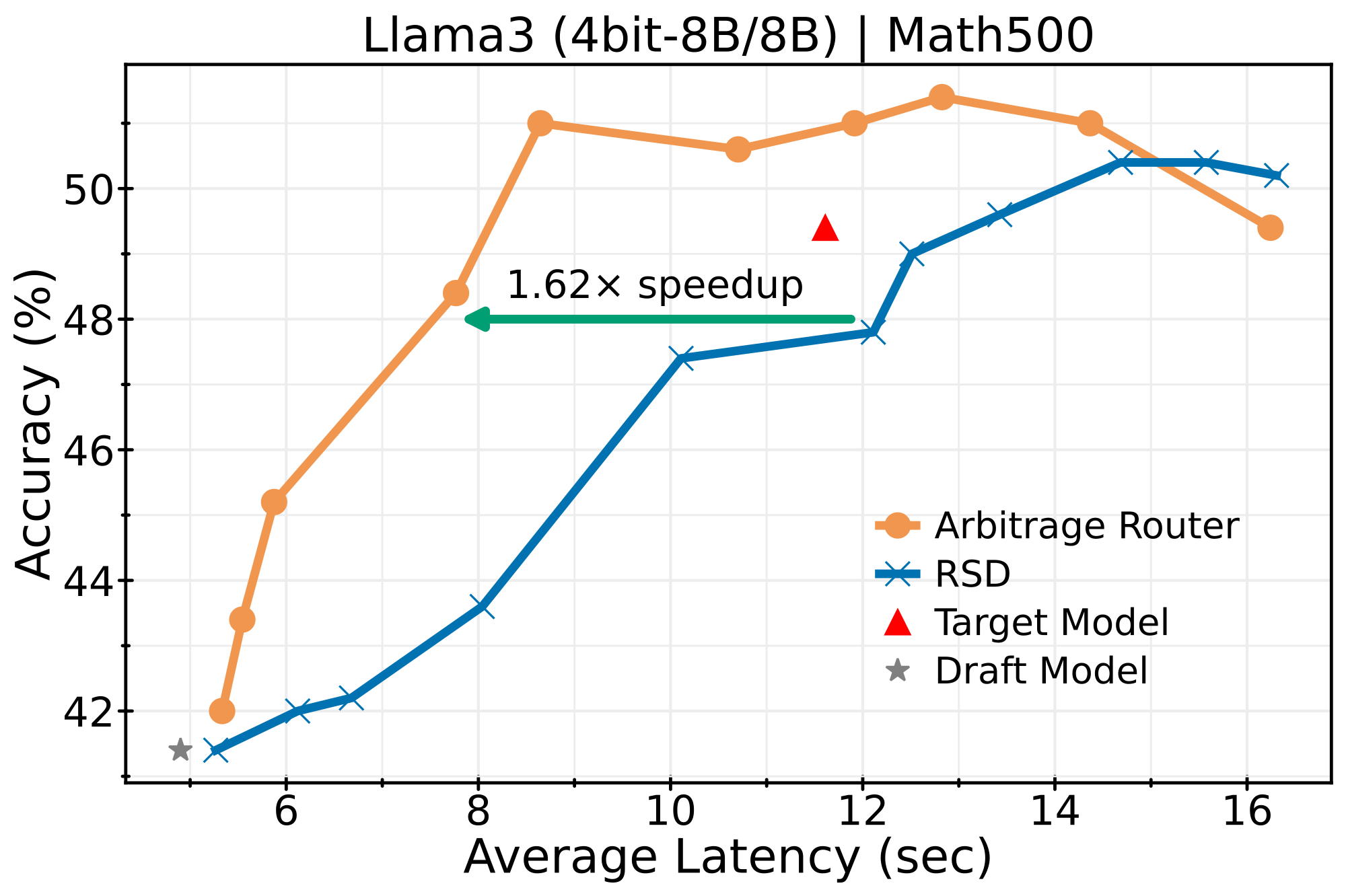
Latency Speedup

Wall-clock time comparison showing Arbitrage achieves better accuracy-latency trade-offs:

Speedup on MATH500 — MATH500: Quantized 8B → 8B

Speedup on OlympiadBench — OlympiadBench: 1B → 8B

Citation

@misc{maheswaran2025arbitrageefficientreasoningadvantageaware,
title={Arbitrage: Efficient Reasoning via Advantage-Aware Speculation},
author={Monishwaran Maheswaran and Rishabh Tiwari and Yuezhou Hu and Kerem Dilmen and Coleman Hooper and Haocheng Xi and
Nicholas Lee and Mehrdad Farajtabar and Michael W. Mahoney and Kurt Keutzer and Amir Gholami},
year={2025},
eprint={2512.05033},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2512.05033},
}